유사 Gooch 셰이딩 모델 구현하기

들어가기

최근 실시간 렌더링에 대한 관련 책을 하나 읽고 있다. 다만, 이론적인 내용을 오직 글로만 학습하는 것은 제법 따분한 일이다. 단순히 읽기만 해서는 좀처럼 흥미가 잘 생기지 않아서, 실제 구현 결과는 어떤 식으로 나타나는지 호기심이 생겨 간단한 실습을 해보기로 했다. 이번 포스트에서 다룰 것은 Gooch 셰이딩에 기반한 형태의 간단한 셰이딩 모델의 구현이다.

Gooch 셰이딩

Gooch 셰이딩은 비사실주의 렌더링의 하나로, cool to warm 셰이딩으로도 알려져 있다. Gooch 셰이딩이라는 이름 자체는 Amy Gooch에 의해 개발되었기 때문이다. (사진 출처 - Wikipedia)

Gooch 셰이딩은 크게 두 가지의 색상을 사용하는데, 이는 각각 Warm과 Cool로, warm(ex. 노란색)은 광원을 향하는 표면을 나타내고, cool(ex. 파란색)은 그 반대쪽을 향하는 표면을 나타낸다.

보통 두번의 패스에 걸쳐 그려지는 경우가 많은데, 위의 그림에서 볼 수 있듯, 먼저 cool to warm 셰이딩을 수행한 후, 검은 색의 외곽선을 그려주는 것이 그 예다.

셰이딩 모델 정의

이번 포스트에서 구현할 셰이딩 모델은, Gooch 셰이딩과 유사하지만, 다중 광원에 대해 동작이 가능하도록 수정된 형태이다. (비록 여기서는 하나의 광원만을 사용하더라도)

사실은, uint 유니폼을 활용하여 실제로 여러 개의 광원을 넣을 수 있는 형태로 구현을 하려 했는데, 생각대로 되지 않아 궁금한 맘에 포럼에 질문을 올렸다. 알고보니 ShaderMaterial의 uint 유니폼 설정과 관련한 버그가 있었고, 그걸 어쩌다 내가 찾았던 모양이다. 직접 PR을 올린건 아니지만, 이슈를 발견함에 따라 간접적으로 라이브러리에 기여했다는 생각에 뿌듯한 경험이었다.

먼저 여기서 사용될 각 벡터에 대해서는 아래의 그림이 이해를 도울 것이다.

여러 개의 광원이 적용된 기초 셰이딩 모델의 수식은 다음과 같은 형태가 된다.

$$c_{shaded} = f_{unlit}(n,v) + \sum_{i=1}^{n}(l_{i} \cdot n)^{+}c_{light_i}f_{lit}(l_{i},n,v)$$

단, 이번 구현에서는 편의 상 여러 개의 광원을 두지 않고, 단 하나의 광원으로 처리한다. 따라서, 아래와 같이 단순화할 수 있다.

$$c_{shaded} = f_{unlit}(n,v) + (l \cdot n)^{+}c_{light}f_{lit}(l,n,v)$$

여기서, Gooch 모델과 유사한 형태로 보이기 위해 다음과 같이 lit과 unlit 항을 둔다.

$$f_{unlit}(n,v)=\frac{1}{2} c_{cool}$$ $$f_{lit}(l, n, v) = s \cdot c_{highlight} + (1 - s)c_{warm}$$

여기에, 다음과 같은 중간 계산 과정이 추가된다.

$$c_{cool} = (0,0,0.55) + 0.25c_{surface}$$ $$c_{warm} = (0.3,0.3,0) + 0.25c_{surface}$$ $$c_{highlight} = (2,2,2)$$ $$r = 2(n \cdot l)n - l$$ $$s = (100(r\cdot v) - 97)^\mp$$

구현해보기

구현에 있어서는 BabylonJS의 ShaderMaterial을 사용했고, 셰이더를 적용할 메쉬로는 수잔을 사용했다. BabylonJS에 관련된 코드는 이 포스트에서 중점적으로 다루고 싶은 바가 아니므로 생략하고 셰이더 코드와 관련된 부분들만 다루고자 한다.

버텍스 셰이더

버텍스 셰이더에서는 정점의 위치와 법선을 전역 공간으로 변환하여 각각 vPosition과 vNormal이라는 이름으로 프래그먼트 셰이더에 넘긴다. 또한 정점을 클립 공간으로 변환하여 gl_Position으로 넘겨준다. BabylonJS에서는 빌트인 유니폼으로 world, worldViewProjection 등을 제공하므로, 작성에 큰 어려움이 없다.

#version 300 es
precision highp float;

in vec3 position;
in vec3 normal;

uniform mat4 world;
uniform mat4 worldViewProjection;

out vec3 vPosition;
out vec3 vNormal;

void main(){
  vPosition=mat3(world)*position;
  vNormal=mat3(world)*normal;
  gl_Position=worldViewProjection*vec4(position,1.);
}

이렇게 넘긴 vPosition과 vNormal은 보간되며, 전역 좌표계와 함께 컬러를 통해 확인해보면 아래와 같다.

바로 아래는 vPosition이고,

그 아래는 vNormal이다.

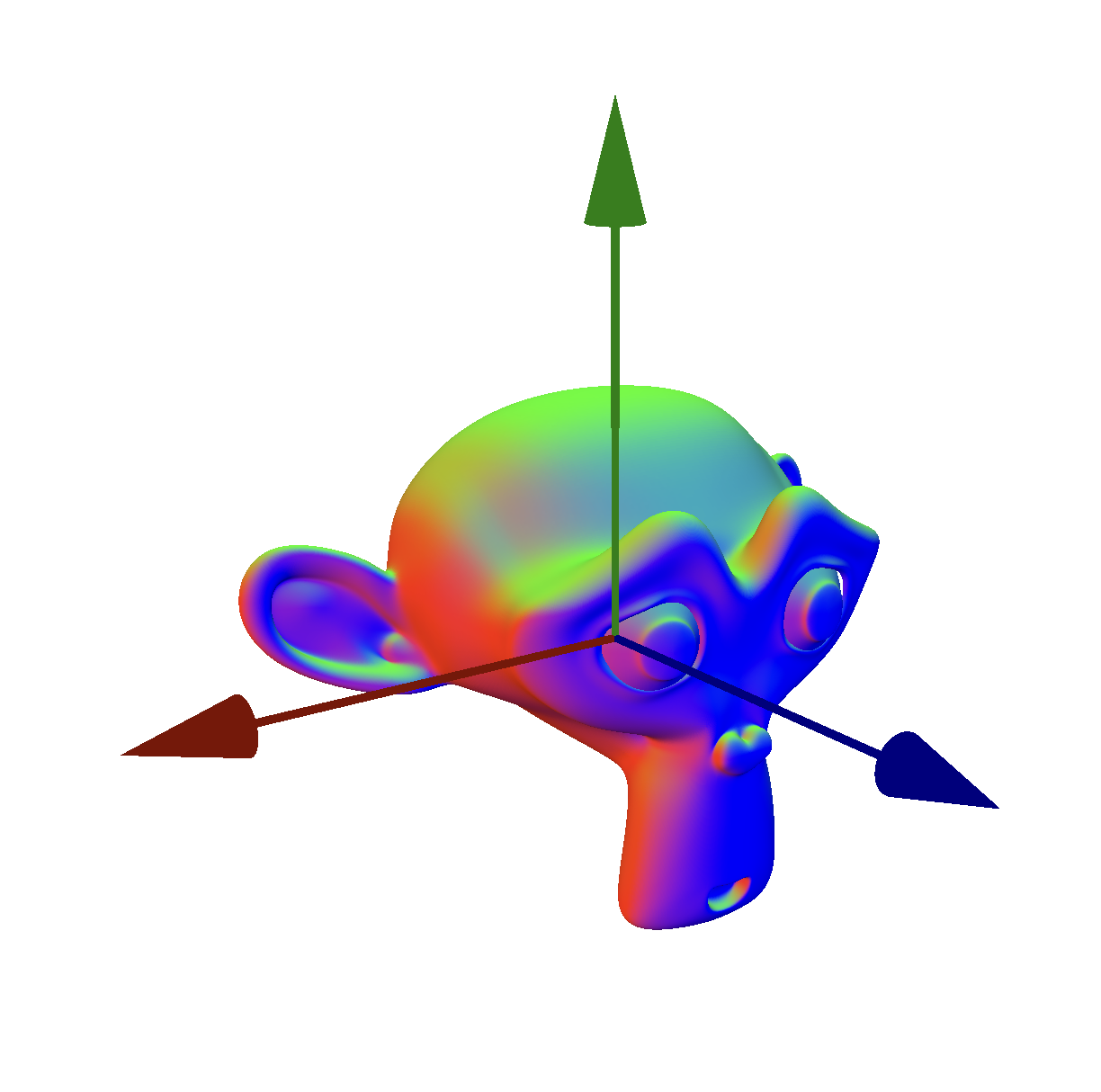
프래그먼트 셰이더

여기서 식을 다시 살펴보자.

$$c_{shaded} = f_{unlit}(n,v) + (l \cdot n)^{+}c_{light}f_{lit}(l,n,v)$$

먼저, 빛을 받지 못하는 부분인 $f_{unlit}$ 에 대한 구현을 먼저 수행할 것이다. 아래의 중간 계산을 처리해주면 된다.

$$f_{unlit}(n,v)=\frac{1}{2} c_{cool}$$ $$c_{cool} = (0,0,0.55) + 0.25c_{surface}$$

위의 식에는 $n, v$ 가 매개변수로서 들어있지만, 실제로 사용되지는 않으므로 코드 작성에서는 제외한다.

// ...

uniform vec3 coolColor;
uniform vec3 surfaceColor;

// ...

vec3 unlit(){
  vec3 c=coolColor+.25*surfaceColor;
  return c*.5;
}

다음으로, 빛을 받는 부분인 $f_{lit}$ 에 대한 구현을 수행한다. 아래의 중간 계산을 처리해주면 된다.

$$f_{lit}(l, n, v) = s \cdot c_{highlight} + (1 - s)c_{warm}$$ $$c_{warm} = (0.3,0.3,0) + 0.25c_{surface}$$ $$c_{highlight} = (2,2,2)$$ $$r = 2(n \cdot l)n - l$$ $$s = (100(r\cdot v) - 97)^\mp$$

// ...

uniform vec3 warmColor;
uniform vec3 surfaceColor;
uniform vec3 highlightColor;

vec3 lit(vec3 l,vec3 n,vec3 v){
  vec3 rl=reflect(-l,n);
  vec3 c=warmColor+.25*surfaceColor;
  float s=clamp(100.*dot(rl,v)-97.,0.,1.);
  return mix(c,highlightColor,s);
}

여기서, reflect(i, n)는 입사 벡터의 반사 벡터를 구하는 계산식인 i - 2.0 * dot(n, i) * n을 처리해주는 빌트인 함수다. 단, 여기서 코드 내 l은 입사 벡터가 아닌, 광원 쪽을 향하는 방향 벡터이므로, 이에 대한 역(-l)을 취해주어야 한다는 점에 주의할 필요가 있다.

s는 하이라이트 혼합 계수를 구하는 것으로, 반사광 rl과 관측 벡터 v의 내적을 통해 두 벡터 간의 서로 정렬되는 정도를 구하여 이를 적절히 활용하며, 그 결과를 0 ~ 1 사이의 값으로 클램핑해준다.

이제 나머지는 이렇게 만든 각 함수를 통해 아래의 완전한 식을 계산해주기만 하면 된다.

$$c_{shaded} = f_{unlit}(n,v) + (l \cdot n)^{+}c_{light}f_{lit}(l,n,v)$$

// ...

uniform vec3 cameraPosition;
uniform vec3 lightPosition;
uniform vec3 lightColor;

// ...

in vec3 vPosition;
in vec3 vNormal;

out vec4 outColor;

void main(){
  vec3 unlitColor=unlit();
  outColor=vec4(unlitColor,1.);
  vec3 n=normalize(vNormal);
  vec3 v=normalize(cameraPosition-vPosition);
  vec3 l=normalize(lightPosition-vPosition);
  float dl=clamp(dot(n,l),0.,1.);
  outColor.rgb+=dl*lightColor*lit(l,n,v);
}

구현 결과

마치며

따분하게 느껴졌던 이론을 실제로 적용해보고 구현하는 일련의 경험은 언제나 즐겁다. 이번 포스트에서는 Gooch 셰이딩과 유사한 형태의 간단한 셰이딩 모델을 구현해보았고, 기본적인 셰이딩 모델을 구현하는 방식에 대한 이해를 높일 수 있었다.