PBR (Physically Based Rendering)

들어가기

컴퓨터 그래픽스와 3D 모델링 분야에서 현실감 있는 이미지를 생성하는 것은 오랜 기간 동안 주요 목표 중 하나였습니다.

이를 위해 다양한 렌더링 기법들이 개발되어 왔고, 그 중 이번 포스트에서 다루고자 하는 PBR은 빛의 물리적 특성을 기반으로 재질의 반사/굴절/흡수 등을 시뮬레이션 하여 현실에 가까운 이미지를 구현하는 기술입니다.

alt text

물리학적인 개념에 기반을 두어 현실에 가까운 묘사가 가능하다는 점에서, 오늘날 대부분의 현실적인 그래픽을 전달하고자 하는 많은 류의 게임과 영상 분야에서는 PBR이 활용됩니다.

What's PBR?

PBR(Physically Based Rendering)은 물리적 세계와 밀접하게 일치하는 기본 이론을 바탕으로 하는 렌더링 기법입니다. PBR은 실제 빛을 모방하는 것을 목표로 하기 때문에, 일반적으로 기존의 알고리즘에 비해 더 사실적으로 보입니다.

아래 두 스크린샷 중 위는 PBR을 통해 구현한 구이고, 아래는 대표적인 non-PBR 셰이딩 중 하나인 Phong 셰이딩으로 구현한 구입니다.

alt text

특히 PBR의 가장 큰 장점은, 조명의 배치와 크게 관계없이 올바른 형태로 보인다는 점인데, non-PBR 파이프라인에서는 그렇지 않습니다.

하지만 여전히 PBR은 물리적 원리에 대한 근사치를 기반으로 한 렌더링이기 떄문에, 물리적 셰이딩(Physical Shading)이 아니라, 물리 기반 셰이딩(Physically Based Shading)이라는 명칭을 씁니다.

반사율 방정식 (Reflectance Equation)

PBR에 대한 이해는 아래와 같은 반사율 방정식(Reflectance Equation)에서 출발합니다.

$L_o(p, \omega_o) = \int_{\Omega} f_r(p, \omega_i, \omega_o) L_i(p, \omega_i) (n \cdot \omega_i) \, d\omega_i$

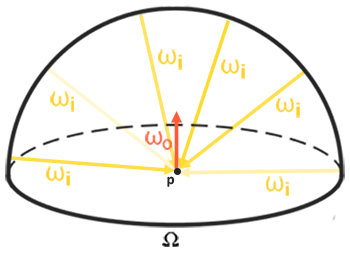
반사율 방정식은, 모든 방향에서 들어오는 빛의 입력 광원을 반구 전체에 걸쳐 적분하여 표면의 한 지점이 주어질 때 특정 시야 방향에서 수신되는 출력 광량(= 보이는 빛의 양)을 나타냅니다.

$L$ : Radiance (복사휘도/방사휘도), 특정 지점에서 들어오거나 나가는 빛의 양에 대한 측정입니다.
$\Omega$ : Hemisphere (반구), 노멀 벡터 $n$ 을 기준으로 한 모든 입사 방향 $\omega_i$ 의 집합
$\omega_i$ , $\omega_o$ : 각각 입사/출사 방향 벡터

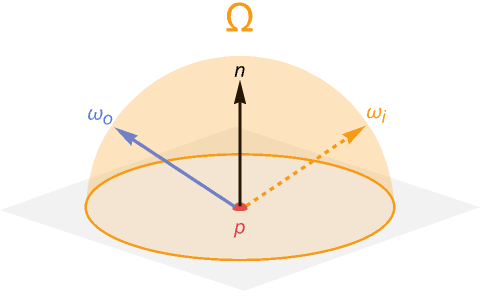
alt text

PBR은 이 반사율 방정식에 기반하여 각각에 대한 근사치를 구하여 셰이더에 녹여내는 과정에 가깝습니다. 즉, PBR은 이 반사광을 실제처럼 묘사하고자 하는 노력이라고 볼 수 있습니다.

BRDF (Bidirectional Reflective Distribution Function, 양방향반사도분포함수)

BRDF는 입사벡터(빛) $\omega_i$ , 출사벡터(뷰) $\omega_o$ , 표면 법선 $n$ , 표면 파라미터 $a$ 를 통해 빛이 불투명한 표면에서 어떤 방식으로 반사되는지에 대해 정의하는 함수입니다. BRDF는 재질의 속성에 따라 들어오는 빛 $\omega_i$ 각각이 최종적으로 표면에서 반사되는 빛에 얼마나 기여하는지에 대해 근사합니다. 즉, 쉽게는 재질의 특성을 반영하는 함수라고 볼 수 있습니다.

Smoothness and roughness

앞선 반사율 방정식에서 BRDF는 아래의 부분에 해당합니다.

$f_r(p, \omega_i, \omega_o)$

오늘날에 실시간으로 PBR 파이프라인을 구축하기 위해 활용되는 대부분은 Cook-Torrance BRDF로 불리는 BRDF를 사용합니다.

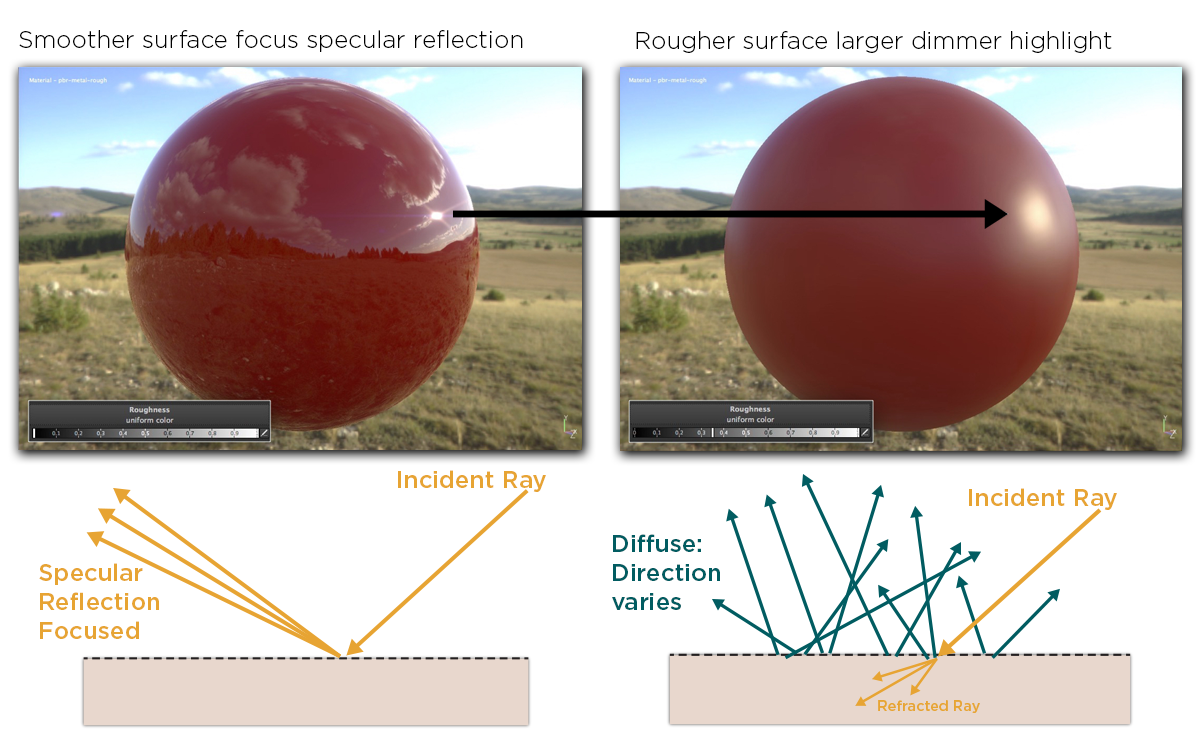
Cook-Torrance BRDF는 Diffuse(난반사광/확산광/분산광)과 Specular(정반사광/반사광) 두 부분으로 나뉘게 됩니다.

$f_r = k_d f_{lambert} + k_s f_{cook-torrance}$

이 중 $k_d$ 는 입사하는 빛에 대해 굴절(refraction)되는 비율이고, $k_s$ 는 반사(reflection)하는 비율입니다.

$Reflection and Refraction$

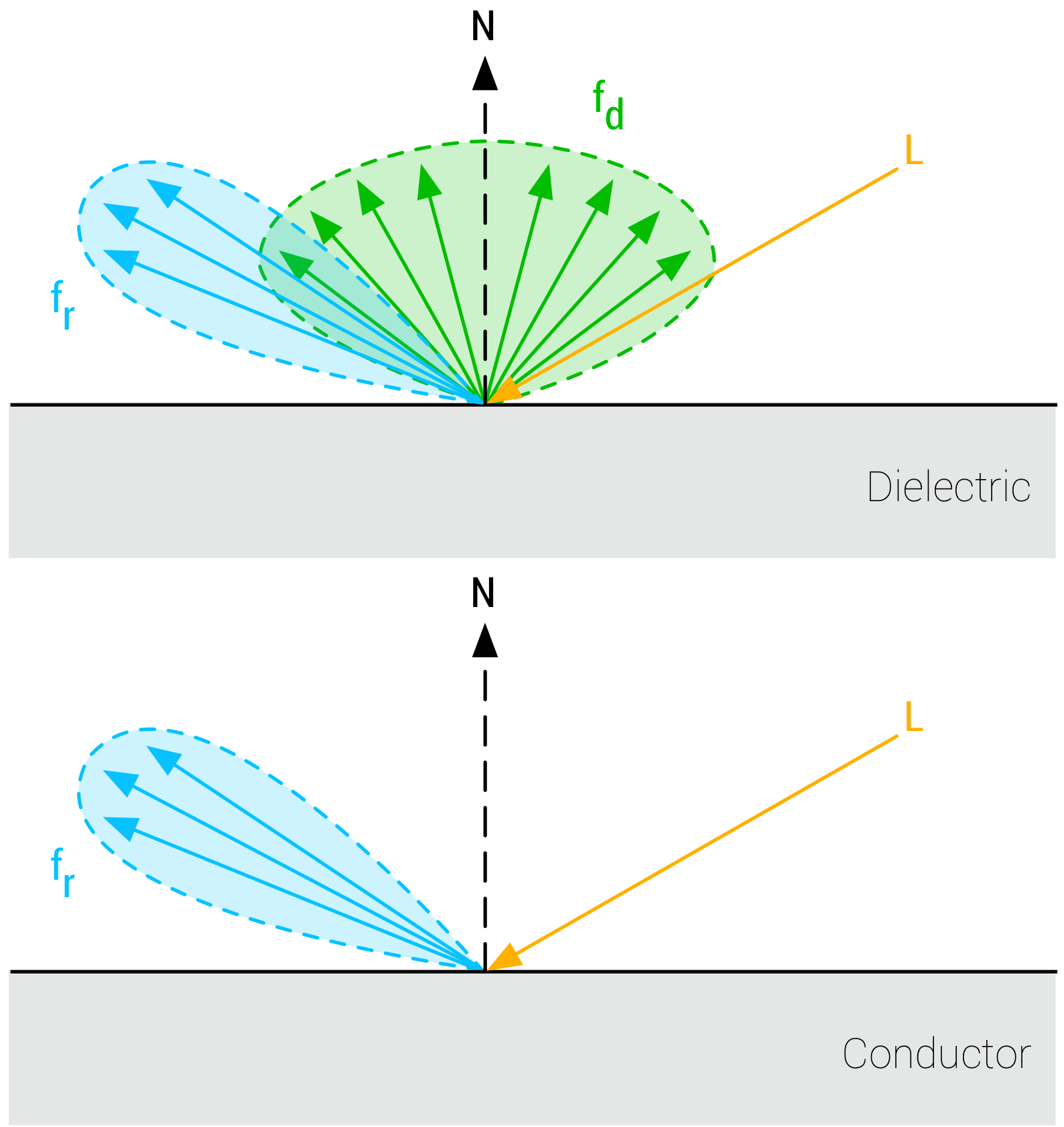
alt text

Diffuse 파트는 램버트 디퓨즈(Lambertian diffuse)로, 상수로 다루어지는 diffuse 입니다.

여기서의 $c$ 는 표면의 색이 되며, $\pi$ 로 나누어 각각의 입사벡터에 대해 정규화시킵니다.

$f_{lambert} = \frac{c}{\pi}$

남은 부분은 Specular 파트인데, 세 가지 함수( $D$ , $F$ , $G$ )와 분모의 정규화 계수로 구성됩니다.

$f_{cook-torrance} = \frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)}$

각각의 함수는 표면 반사의 각 특성을 근사화하는 함수 유형을 나타내며, 각각 아래를 의미합니다. 각각 어떤 의미를 갖는지에 대해서도 깊게 들여다보면 좋겠지만, 분량 문제로 인하여 아래쪽의 참조 문서로 대체하도록 하겠습니다.

$D$ : Normal Distribution Function (정규 분포 함수)
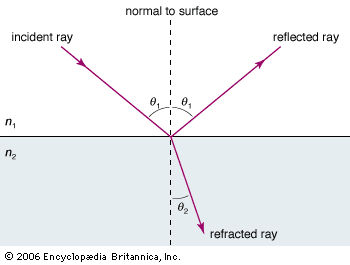
$F$ : Fresnel Equation (프레넬 방정식)
$G$ : Geometry Function (지오메트리 함수)

여기까지 알게 되었다면, 이제 반사율 방정식을 보다 구체화할 수 있습니다.

$L_o(p, \omega_o) = \int_{\Omega} f_r(p, \omega_i, \omega_o) L_i(p, \omega_i) (n \cdot \omega_i) \, d\omega_i$ $L_o(p, \omega_o) = \int_{\Omega} (k_d f_{lambert} + k_s f_{cook-torrance}) L_i(p, \omega_i) (n \cdot \omega_i) \, d\omega_i$ $L_o(p, \omega_o) = \int_{\Omega} (k_d \frac{c}{\pi} + k_s \frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)}) L_i(p, \omega_i) (n \cdot \omega_i) \, d\omega_i$

Image Based Lighting (IBL)

자, 이렇게 방정식에 대해 알게 되었지만, 실시간으로 그래픽을 그려내야 한다는 관점에서는 아래의 두 부분이 여전히 문제가 됩니다.

주어진 방향 벡터 $\omega_i$ 에 대해 Radiance( $L_i$ )을 계산할 방법이 있어야 합니다.
위의 방정식에 대한 계산이 실시간으로 이루어져야 합니다.

Radiance

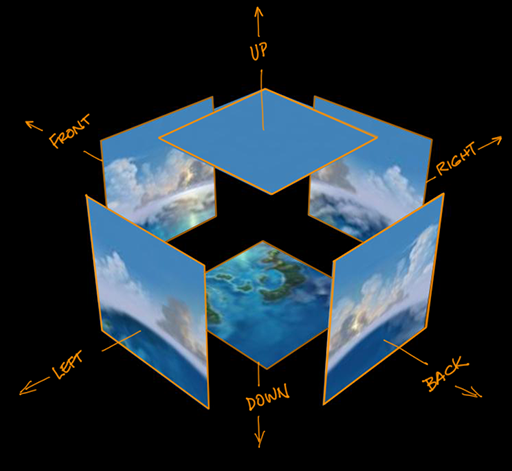
이 중, 첫번째 문제의 해결을 위한 키 포인트는 큐브맵(CubeMap)을 활용하는 것입니다. 큐브맵을 하나의 단일 광원처럼 사용하고, 이를 주어진 방향 벡터 $\omega_i$ 에 대해 샘플링하면 $L_i$ 을 구할 수 있습니다.

Cube Map Example

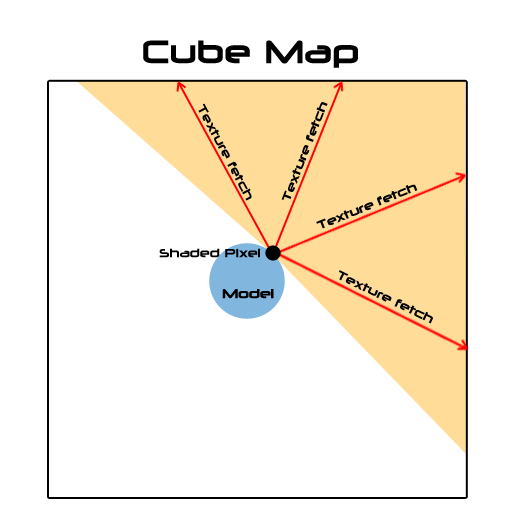
하지만, 적분의 해결을 위해서는 반구 위 가능한 모든 방향 $\omega_i$ 에 대해서 계산이 수행되어야 하는데, 이를 실제로 적용하는 것은 대단히 비용이 많이 드는 일이기 때문에 실시간 계산이 어렵습니다. 그렇기 때문에 이에 대한 해결책을 Diffuse와 Specular 각각에 대해 제시해야 합니다.

Diffuse

이 시점에서 방정식을 다시 한번 들여다봅시다.

$L_o(p, \omega_o) = \int_{\Omega} (k_d \frac{c}{\pi} + \frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)}) L_i(p, \omega_i) (n \cdot \omega_i) \, d\omega_i$

이 중 Diffuse 항을 잘 보면, 이것이 적분 변수 $\omega_i$ 에 의존하고 있지 않으며, 상수항에 해당한다는 점을 알 수 있습니다.

그렇기 때문에 이를 적분에서 분리할 수 있습니다.

$L_o(p, \omega_o)_{diffuse} = k_d \frac{c}{\pi} \int_{\Omega} L_i(p, \omega_i) (n \cdot \omega_i) \, d\omega_i$

이제 적분이 의존하는 변수는 $\omega_i$ 뿐이기 때문에, 컨볼루션(Convolution)을 통해 각 샘플 벡터(=텍셀, Texel)에 저장되는 새로운 큐브맵을 미리 계산할 수 있습니다. (pre-compute)

컨볼루션은 데이터 셋의 다른 모든 항목을 고려해 데이터 셋 각 항목에 일부 연산을 적용하는 것으로, 여기서의 데이터 셋은 장면의 광원 또는 환경 맵(Environment Map)이 됩니다.

alt text

이렇게 미리 계산을 마친 큐브맵에는 각 $w_o$ 샘플에 대한 적분 결과가 저장됩니다.

vec3 irradiance = vec3(0.0);  

vec3 up    = vec3(0.0, 1.0, 0.0);
vec3 right = normalize(cross(up, normal));
up         = normalize(cross(normal, right));

float sampleDelta = 0.025;
float nrSamples = 0.0; 
for(float phi = 0.0; phi < 2.0 * PI; phi += sampleDelta)
{
    for(float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta)
    {
        // spherical to cartesian (in tangent space)
        vec3 tangentSample = vec3(sin(theta) * cos(phi),  sin(theta) * sin(phi), cos(theta));
        // tangent space to world
        vec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N; 

        irradiance += texture(environmentMap, sampleVec).rgb * cos(theta) * sin(theta);
        nrSamples++;
    }
}

irradiance = PI * irradiance * (1.0 / float(nrSamples));

이렇게 만든 Irradiance Map은 아래와 같은 형태가 됩니다.

Irradiance map example

이제 이렇게 구한 Irradiance를 기반으로 Diffuse를 적용할 수 있게 되었습니다. 모델에 Diffuse가 적용된 결과를 렌더링 해보면, 환경 맵에 따라 조화로운 형태로 Diffuse가 적용되는 것을 확인해볼 수 있습니다.

Diffuse Example1

Diffuse Example2

Specular

남은 것은 Specular인데, 앞선 방정식에서 Specular 항을 다시 살펴봅시다.

$L_o(p, \omega_o)_{specular} = \int_{\Omega} \frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)} L_i(p, \omega_i) (n \cdot \omega_i) \, d\omega_i$

Specular의 경우는 Diffuse보다 좀 더 까다롭습니다. 기본적으로 입사/반사의 두 벡터에 의존하는 형태로 구성되어 있기 때문입니다. 언리얼 엔진의 개발사인 Epic Games에서는 이 문제를 각각 두개의 식으로 쪼개서 미리 계산을 수행한 다음, 최종 결과에 이를 합치는 방식으로 해결합니다.

이러한 관점을 갖고 바라볼 때, 위 방정식은 아래와 같은 형태로 쪼개질 수 있습니다.

$L_o(p, \omega_o)_{specular} = \int_{\Omega} L_i(p, \omega_i) * \int_{\Omega} \frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)} (n \cdot \omega_i) \, d\omega_i$

앞쪽 항의 경우, Diffuse의 경우와 유사하게 컨볼루션을 통해 해결할 수 있습니다. Specular의 경우 재질의 거칠기(roughness)에 따라 흐릿함의 정도에 차이가 발생하기 때문에, roughness 수준에 따라 활용할 목적으로 밉맵(Mip Map)의 형태로 생성합니다.

Prefiltered Map

사실 반사광에 대해 정확하게 구현하고 사전 필터링을 하려면 뷰 벡터 $V$ 에 대한 정보가 있어야 합니다.

하지만, 실제 렌더링을 하기도 전에 사전 계산을 수행하는 시점에서는 뷰 벡터에 대한 정보가 없습니다. 이에 따라 출력 샘플 벡터 $\omega_i$ 가 뷰 벡터 $V$ 와 동일하다고 가정합니다. 이에 따라 법선/반사/뷰 벡터가 모두 동일해지기 때문에( $V=R=N$ ) 이를 통해 사전 필터링 단계에서 뷰 벡터에 대한 정보 자체가 필요없게 만듭니다.

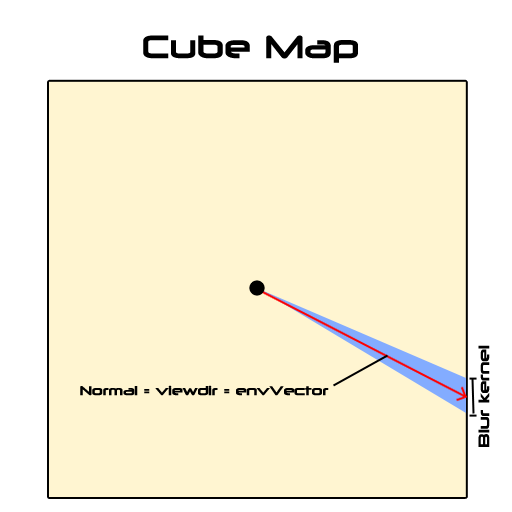
alt text

이에 따라 완전한 형태과 비교하여 시각적인 차이는 생기지만, 충분히 용인 가능한 형태의 표면 반사를 그려낼 수 있습니다.

V = R = N

남은 항은 Specular 적분의 BRDF 부분인데, BRDF 역시 모든 방향에서 들어오는 Radiance가 완전한 백색이라는 가정을 둔다면 미리 계산이 가능합니다.

이렇게 미리 계산한 BRDF 텍스처를 BRDF LUT(Look Up Table)이라고 합니다.

이 LUT는 법선 벡터 $N$ 과 뷰 벡터 $V$ 에 대한 내적값을 x축, roughness 값을 y축으로 두고 R색상을 scale로, G색상을 bias로 활용하는 BRDF를 구할 수 있게 됩니다.

BRDF LUT Example

이제 이 사전 계산된 두 결과 텍스처들을 통해 마침내 아래와 같이 Specular를 근사할 수 있게 되었습니다.

vec3 F = fresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);

const float MAX_REFLECTION_LOD = 10.0;
vec3 prefilteredColor = textureLod(prefilterMap, R,  roughness * MAX_REFLECTION_LOD).rgb;    
vec2 brdf  = texture(brdfLUT, vec2(max(dot(N, V), 0.0), roughness)).rg;
vec3 specular = prefilteredColor * (F * brdf.x + brdf.y);

결과물

이렇게 구한 Diffuse와 Specular를 활용하여 렌더링을 수행해내면 비로소 이와 같은 결과물을 얻을 수 있게 됩니다.

비물리 기반 렌더링에 해당하는 Phong과 비교하여 주변 환경이 반영된 결과에 따라 부여된 현실감이 눈에 띕니다.

alt text

마치며

PBR에 대해서는 예전부터 살펴보고 싶었으나, 어려워 보인다는 이유로 계속 미루고 미루었던 주제였습니다. 실제로 이를 익히기 위해 살펴봐야 하는 정보의 양과 깊이가 대단히 엄청남을 느낄 수 있었습니다. 분량 문제로 인하여 상세하게 다루지 못한 부분도 많고, 어중간한 이해로 넘어간 부분도 많다는 느낌이 들지만, 어찌저찌 볼 수 있는 결과물로 그려내고 나니 새삼 뿌듯한 것 같습니다.

Shubidumdu

Posts

Projects

Sketchbook

2024-05-19

PBR (Physically Based Rendering)

들어가기

What's PBR?

반사율 방정식 (Reflectance Equation)

BRDF (Bidirectional Reflective Distribution Function, 양방향반사도분포함수)

Image Based Lighting (IBL)

Diffuse

Specular

결과물

마치며

참고